Introduction
Geometry is an essential branch of mathematics that explores the properties and relationships of shapes and figures. Through detailed explanations, illustrative diagrams, and practical examples, you’ll develop a solid foundation in geometry and enhance your problem-solving skills.
Points, Lines, and Angles:
Point: A location in space with no size or dimension.

Line: A straight path that extends infinitely in both directions.

Line Segment: A part of a line with two endpoints.

Ray: A part of a line with one endpoint and extending infinitely in one direction.

Angles: Learn about different types of angles and their measurements, such as acute, obtuse, and right angles.
Triangles
A closed, three-sided polygon.
Types of Triangles:
(Based on Sides)
Equilateral Triangle: An equilateral triangle has all three sides of equal length.
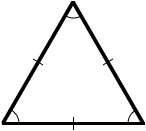
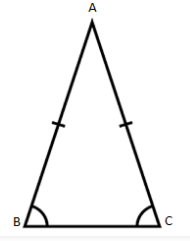
Isosceles Triangle: An isosceles triangle has two sides of equal length and one side of a different length.
Scalene Triangle: A scalene triangle has all three sides of different lengths.
(Based on Angles)
Acute Triangle: An acute triangle has all three angles that are less than 90 degrees.
Obtuse Triangle: An obtuse triangle has one angle that is greater than 90 degrees.
Right Triangle: A right triangle has one right angle (90 degrees).
Angle Sum Property: The sum of angles in a triangle is 180°.
Quadrilaterals:

A closed, four-sided polygon.
There are five main types of quadrilaterals: squares, rectangles, parallelograms, trapezoids, and rhombuses. A square has four equal sides and four right angles. A rectangle has four right angles but not necessarily four equal sides. A parallelogram has opposite sides that are parallel and equal in length. A trapezoid has one set of parallel sides. A rhombus has four equal sides but not necessarily four right angles.
Circles:

Circle: A closed shape with all points equidistant from the center.
Elements of a Circle:
Based on the Points Inside, Outside, or On the Circle:
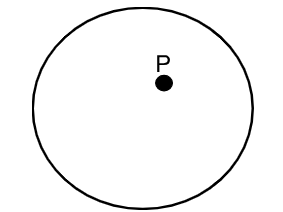
a) Interior of the Circle: The points inside the circle are all the points whose distance from the center is less than the radius.
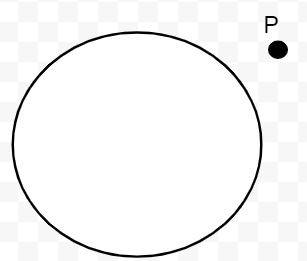
b) Exterior of the Circle: The points outside the circle are all the points whose distance from the center is greater than the radius.
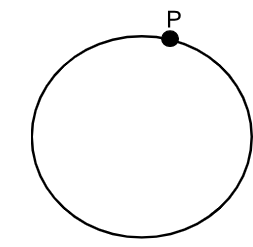
c) Points on the Circle: The points on the circle are all the points whose distance from the center is equal to the radius.
Based on Intersection with Lines:
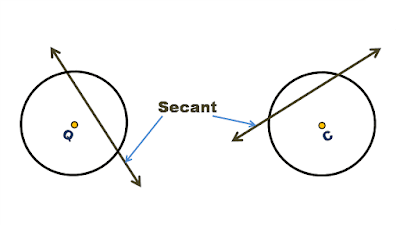
a) Secant: A secant is a line that intersects the circle at two distinct points.
b) Chord: A chord is a line segment that connects two points on the circle.
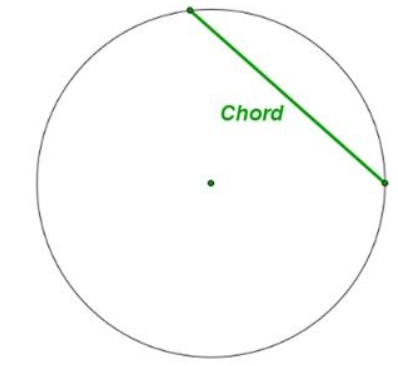
c) Diameter: A diameter is a chord that passes through the center of the circle, dividing it into two equal halves.
d) Circumference: In circles, the circumference is the total length of the boundary or the outer edge of the circle. It is also known as the perimeter of the circle.
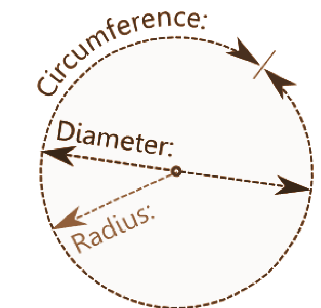
The circumference is calculated by using the formula:
Circumference (C) = 2 × π× radius = 2πr
Where π (pi) is a mathematical constant approximately equal to 3.14159.
e) Radius: The radius is the distance from the center of the circle to any point on its circumference. Also defined as, radius is half of the diameter i.e.,
radius= diameter/2
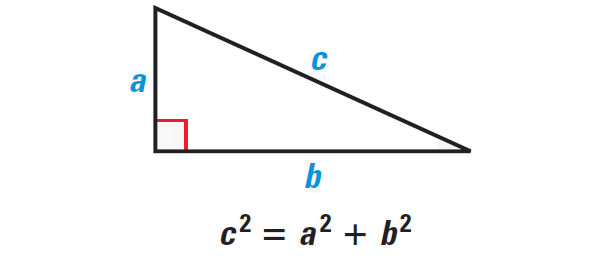
The Pythagorean theorem
The Pythagorean theorem is a mathematical relationship between the three sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Solving geometric problems
There are many different ways to solve geometric problems. Some common methods include:
Using the properties of shapes
Using the Pythagorean theorem
Using similar triangles
Using coordinate geometry
Geometry in real-world problems
Geometry is used in many real-world problems. For example, we might use geometry to design a building, to lay out a garden, or to solve a construction problem. We might also use geometry to analyze the motion of objects, to design machines, or to create art.
Examples
Here are some examples of geometric problems that students might encounter in class 9:
Find the area of a triangle
Find the volume of a cube
Determine if two triangles are similar
Solve a construction problem using coordinate geometry
Analyze the motion of an object using geometry
I hope this guide helps you understand geometry for class 9!.
