Introduction
Trigonometry is a crucial branch of mathematics that deals with the relationships between angles and sides of triangles. With this comprehensive guide, you will delve into trigonometric ratios, identities, and their practical implications. It is used in many different fields, such as engineering, surveying, and navigation.
How to Find Trigonometric Ratios?
Let’s assume the right triangle, right-angled at B as θ (theta), and the sides are labeled as follows:
Opposite side (O): The side opposite to the angle θ.
Adjacent side (A): The side adjacent to the angle θ but not the hypotenuse.
Hypotenuse (H): The side opposite the right angle and the longest side of the right triangle.
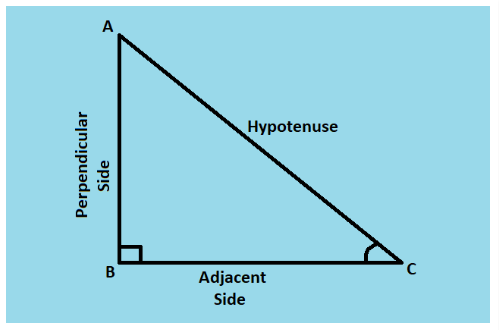
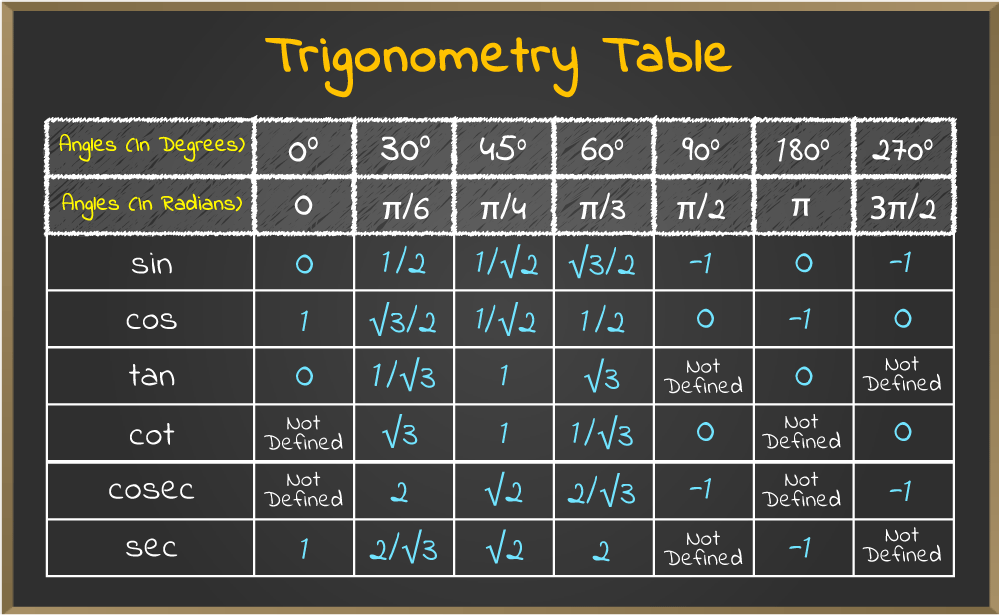
The Trigonometric ratios are defined as follows:
The three main trigonometric ratios are sine, cosine, and tangent.
- Sine is the ratio of the opposite side to the hypotenuse, i.e.
Sinθ = Opposite side/Hypotenuse - Cosine is the ratio of the adjacent side to the hypotenuse, i.e.
Cosθ = Adjacent side/Hypotenuse - Tangent is the ratio of the opposite side to the adjacent side.
Tanθ = Opposite side/Adjacent side
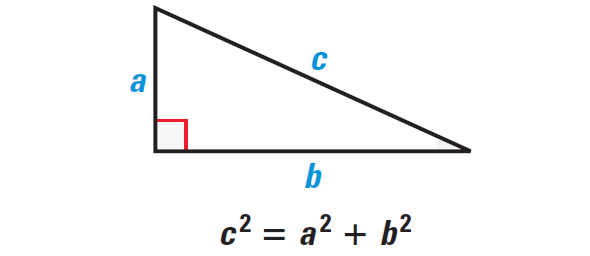
The Pythagorean theorem
The Pythagorean theorem is a mathematical relationship between the three sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Solving trigonometric problems
There are many different ways to solve trigonometric problems. Some common methods include:
- Using the trigonometric ratios
- Using the Pythagorean theorem
- Using the unit circle
Trigonometry in real-world problems
Trigonometry is used in many real-world problems. For example, we might use trigonometry to determine the height of a building, to calculate the distance between two points, or to find the direction of a bearing. We might also use trigonometry to analyze the motion of objects, to design machines, or to create art.
Examples
Here are some examples of trigonometric problems that students might encounter in class 10:
- Find the height of a building using trigonometry
- Calculate the distance between two points using trigonometry
- Analyze the motion of an object using trigonometry
- Design a machine using trigonometry
- Create art using trigonometry
